В теории вероятностей существует классическая задача, известная под разными названиями: задача разборчивой невесты, задача привередливого жениха или задача остановки выбора. С учетом специфики портала Executive.ru назовем ее задачей выбора лучшего кандидата на работу, потому что именно ее каждый день решает HR-менеджер в своей компании.
Условия задачи
- HR-менеджеру необходимо подобрать сотрудника на вакансию.
- На эту должность имеется N кандидатов, и значение N известно.
- Кандидаты проходят собеседование последовательно в случайном порядке, и каждого кандидата можно однозначно оценить по общей для них всех шкале ранжирования, скажем от 0 до 1.
- Решение о приеме или отклонении кандидата основано только на рангах кандидатов, прошедших собеседование к данному моменту времени.
- Сразу после собеседования прошедший его кандидат либо безвозвратно отклоняется, либо принимается на вакансию, и это решение является окончательным. В случае принятия положительного решения по кандидату – собеседование кандидатов останавливается.
- Нужно найти общее решение, состоящее в выработке оптимальной стратегии, гарантирующей выбор лучшего кандидата из всей группы N с наибольшей вероятностью. Другими словами – стратегия должна максимизировать ожидаемый выигрыш.
HR-менеджер выигрывает, когда принимает лучшего кандидата из N.
Впервые эта задача была опубликована Мартином Гарднером в журнале Scientific American за февраль 1960 года. Хотя до того ей уже уделялось большое внимание в научных кругах. На тему ее решения написаны целые тома. В том числе – по различным модификациям этой задачи, например, когда заранее неизвестно общее количество кандидатов N.
Примечательно, что в докторской диссертации Бориса Березовского, известного бизнесмена и политического деятеля, впоследствии члена-корреспондента РАН, на соискание ученой степени доктора наук «Разработка теоретических основ алгоритмизации принятия предпроектных решений и их применения», защищенной в 1983 году, рассматривается обобщение нашей задачи о разборчивой невесте.
Решение
Для решения этой задачи можно применять различные подходы. В силу их сложности и громоздкости приводить здесь я их не буду – при желании подробности можно найти в сети. Не вдаваясь в математические выкладки и доказательства, приведу сразу решение этой замечательной задачи.
Оптимальная стратегия найма выглядит так: отсобеседовать N/e первых кандидатов, где e=2,71828 – число Эйлера или основание натурального логарифма, а затем выбрать из оставшихся первого, который окажется лучше всех предыдущих.
Предположим, что HR-менеджер отобрал 8 резюме кандидатов, которые по его мнению соответствуют вакансии и требованиям компании. Следовательно, N в нашей формуле = 8.
Далее HR-менеджер:
- Провел собесдеования с первыми N/e = 8/2,71828... = 2,9430... ≈ 3 кандидатами, пока не принимая никаких решений.
- Зафиксировал для себя максимальный ранг среди отсобеседованных кандидатов. Предположим, первые 3 кандидата имели ранги 0,4; 0,25; 0,6. И тогда максимальным рангом будет 0,6.
- Продолжает собеседовать кандидатов далее до момента, пока не попадется кандидат с рангом больше 0,6. Именно этому кандидату сделать предложение о работе, а дальнейшие собеседования не проводить.
Описанное выше решение подходит для стратегии выбора лучшего кандидата. С увеличением числа кандидатов N вероятность выбора лучшего кандидата стремится к 1/e = 36,8...%. Не густо?
Расширим условия задачи
Предположим, что HR-менеджер руководствуется менее строгим выбором: согласен выбрать одного из двух лучших кандидатов. В этом случае:
- Рекрутер должен провести собеседования приблизительно у 34,7% первых кандидатов, не принимая решений, лишь фиксируя их ранги, определив лучшего.
- Из следующих приблизительно 32% кандидатов (вплоть до 66,7% от всех) выбрать того соискателя, который окажется лучше всех предыдущих.
- Из оставшихся 33,3% претендентов соглашаться на выбор и второго по качеству среди уже всех отсобеседованных.
При данном подходе с увеличением числа кандидатов N вероятность выбора одного из двух лучших кандидатов стремится к 57,4%, что уже заметно выше.
Можно было бы пойти дальше и расширить выбор, например, один из трех лучших кандидатов, но не будем усложнять. Во-первых, в реальной жизни HR не принимает решений о найме самостоятельно, а лишь предлагает лучших кандидатов руководителю. Во-вторых, обычно двух лучших кандидатов бывает вполне достаточно для руководителя, чтобы он принял окончательное решение, кого из них принять на работу.
Вывод
После выбора рекрутером лучшего кандидата или одного из двух лучших кандидатов из N отобранных резюме с применением вышеописанных подходов достаточно будет пригласить на финальное собеседование с руководителем именно его и любого другого среди тех, кто прошел собеседование, но минимально уступает «лучшему», если он еще будет находиться в поиске работы к тому моменту и готов будет пройти финальное собеседование с руководителем.
Благодаря такому системному подходу:
- Шансы заполучить на работу в компанию лучшего кандидата будут чрезвычайно высоки.
- Руководитель получит на выбор двух заведомо лучших кандидатов от HR-менеджера.
- Затраты времени HR-менеджера на закрытие вакансии будут существенно снижены, чем при бессистемном интуитивном подборе.
- Риски потерять лучшего кандидата будут минимальными.
Читайте также:













Оптовая цена закупки тоже может зависеть от количества, и это тоже может быть ступенчато.
Поэтому, надо задаться себестоимостью единицы продукции, от превышения которой проводить оптимизацию.
Ступенчатую зависимость плохо напрямую оптимизировать, поэтому лучше задать разные величины себестоимости единицы продукции, и для каждой величины найти оптимальную цену и соответствующее количество сбыта. А уже потом сопоставить соответствует ли полученное количество сбыта выбранной величине себестоимости единицы продукции. Ну и найти согласованный оптимальный вариант.
Может их будет несколько, тогда выбрать предпочтительный.
Провести две гиперболы закона спроса и предложения уже религия не позволяет?
Можно. И в общем именно это и важно в реальной экономике торгового бизнеса. И с учетом общих расходов, конечно.
Но тут цель задачки другая -- выявить способность кандидата находить зависимость спроса (сбыта) от цены, найти производную их произведения и решить уравнение.
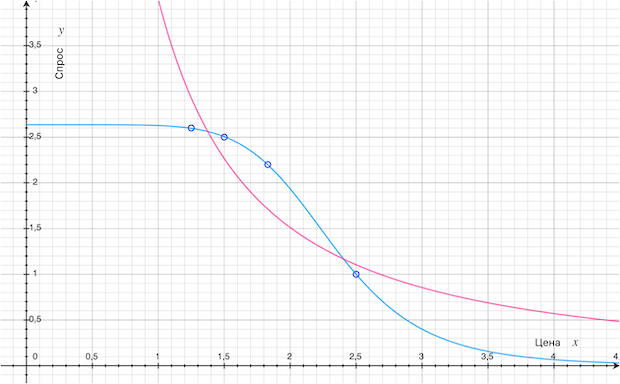
Вообще по классике зависимость спроса (в нашем случае сбыта, если угодно) от цены это малиновая кривая.
Чем ниже цена -- тем выше спрос и наоборот.
Но это необязательно.
В нашем случае заивисмость спроса от цены -- это голубая кривая.
Такое вполне имеет право на жизнь. Когда слишком дешевый товар не покупают, опасаясь низкого качества или подделки.
Или, когда емкость рынка ограничена -- например, если это магазин в маленьком городке -- сельпо.
Или, когда у товара короткий срок годности. Но это скорее фактор сегмента продуктов питания или лекарств.
Где-то выше было указано, что это именно торговля, а не производство? А цена, к примеру, розничная для данного магазина и даты, а не какая-то другая?
Цен много, как и затрат. Каждый в цепочке получит свои цифры и свои зависимости.
Ну кроме прямых затрат есть же еще и косвенные общие -- аренда магаза, например.
Обычно в учете в себстоимость включают только прямые -- расходы на то, чтобы товар оказался у вас на складе.
А все непрямые там просто идут отдельной строкой.
Но вы правы, все по сути сводится к системе сложных уравнений. Параметры которых в той или иной степени зависят друг от друга и переменных и плавают во времени.
Бизнес это математика.
Вообще-то быстрей было бы построить с помощью полинома Лагранжа по 3-м точкам апроксимацию спроса (сбыта) от цены, занести это в Excel и путем расчета с перебором цены подобрать оптимум Выручки.
А определить коэффициенты квадратного многочлена путем решения системы 3-х уравнений с 3-мя неизвестными (коэфициентами) с последующим взятием производной и решением квадратного уравнения заняло больше времени.
Я тут забыл указать, что надо дополнительно проверить стыки участков изменения величины себестоимости, оптимум может в них оказаться.
Из свежего. Это не реклама.
Посмотрите, как крупный виноторговец играет с ассортиментом, производством, закупками, логистикой, позиционированием, запасами и прочим. И так - каждый день. Что-то как-то считается (там, где проще), но далеко не всё.
Разборчивая невеста каждый день прямо с утра начинает выбирать очередного жениха. Оптимально остановиться негде.
https://www.kommersant.ru/doc/5927664?from=author_1
MathCAD и MatLab -- на сегодня это стандарт для работы продуктового аналитика.
Никто уже давно не дифференцирует по правилам вычисления производных.
Порой это бывает невозможно в силу колоссальной сложности уравнений.
Просто берете функцию y=f(x) и дифференцируете y'=d(f(x))/dx.
А если надо получить чистую форму без d/dx то делаете регрессию и аппроксимируете подходящей кривой.
Опять же есть Вольфрам, если нет MathCAD и MatLab.
По ссылке наша выручка от цены.
Вообще-то интегрирование численными методами. На некотором интервале они дают точные результаты, но имеют порог расходимости, для неберущихся интегралов обычно применяют разложение производной в ряд Тейлора и подобные.
Цитирая учебник Жарова, Зальянова, Исакова "Обыкновенные дифференциальные уравнения". Задача эластичности спроса, кстати, находится в 1.3 №23.
При нынешнем уровне прогресса -- всё это мелкие технические вопросы, на мой взгляд :)
Дайте мне любую функцию -- я вам ее продифференцирую, проинтегрирую (по области, по поверхности, по длине), найду корни, экстремумы, итд.
Это не сложно. И не это представляет главный интерес, на мой взгляд.
А интересно исследование свойств наблюдаемых данных, построение точных моделей, эстраполяция, исследование их чувствительности, свойств шума, дифференциация шума и зарождающихся субтрендов, поиск триггеров (ключевого и аномального) влияния, корреляций, распознавание паттернов и понимание их природы.
Тут только опыт и знания в помощь. Чем больше вы с этим работали -- тем точнее будут ваши выводы и прогнозы.
Если ваши прогнозы с завидным постоянством сбываются -- значит вы что-то понимаете.
Будущее одинаково скрыто от всех. Более того оно -- не в полной мере определено. На длинных горизонтах так и подавно.
Здесь НЕТ инсайдов из прекрасного далека ни для кого.
Все сводится к тому, насколько вы глубоко изучили и понимаете предмет наблюдаемого явления. И чем больше связей нашли.
Если хотите что-то доказать -- просто делайте прогнозы и фиксируйте их в публичном поле. Чем точнее ваши выстрелы -- тем объективно выше ваша экспертиза. И как следствие -- авторитет. Все остальное -- пустая болтовня.
И не бойтесь корректировать прогнозы -- прогнозирование оно не про короля горы, а про бизнес в общем-то. И служит цели максимизировать профит. Все сводится к тому -- сколько бабла вы как аналитик сэкономили, или помогли заработать вашему нанимателю.
Стратегия изложенная в статье -- повышает эффективность работы HRа и экономит время компании, и максимизирует шансы заполучить лучших кандидатов.
Не верите? Смоделируйте ее в XLS формулами. И протащите вниз на 10000 строк. И посмотрите какие частоты у вас получатся.
XLS, кстати, хорошо подходит для имитационного моделирования (симуляции) несложных систем.